Tema 15 El color

1. La percepción del color.

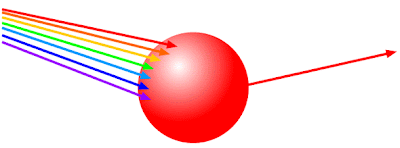
La luz blanca se compone de siete luces de color. Cuando estas luces iluminan un objeto, algunas son absorbidas y otras son reflejadas. Las luces reflejadas son las que podemos ver y las que nos dicen de qué color es el objeto.

2. Los tres parámetros del color.

- Tono. Se refiere al nombre que tiene cada color. Por ejemplo, tono rojo, azul, verde, etc.
- Saturación. Es el grado de pureza del color. Si un color es muy vivo es saturado. Si un color es poco llamativo y se aproxima al gris, al blanco o al negro, es un color desaturado
- Luminosidad o brillo. Es la cantidad de blanco que tiene un color. Los colores blanquecinos son colores luminosos.

3. Colores primarios y secundarios.

Los colores primarios son los que no se pueden obtener por mezcla de otros. Son el amarillo, el azul cyan y el magenta.
Los colores secundarios son los que se obtienen mezclando otros dos, como el rojo o naranja, el verde o el violeta.

4. Colores cálidos y fríos.
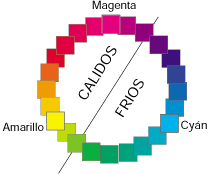
Los cálidos recuerdan al fuego y son el amarillo, naranja, rojo magenta, rosa y marrón.
Los colores fríos son el azul, verde y violeta.

Tema 14. Arte secuencial

1.- Arte secuencial:

El arte secuencial es aquel que se da por medio de imágenes fijas o en movimiento enlazadas entre sí. Este arte es el lenguaje básico de disciplinas como el comic, las fotonovelas o el cine. Las secuencias o conjuntos de imágenes que componen una unidad narrativa, se componen de planos, que son las unidades mínimas de significación.

2.- Tipos de planos o encuadres:

El plano o encuadre es la porción de espacio o personajes que aparece en una viñeta, fotografía, o filmación. Estos son los planos más frecuentes

Gran plano general: Es aquel que toma la vista de la figura humana de un modo muy alejado, mostrando con claridad el espacio en el que ésta se mueve o habita.

Plano general: Similar al anterior, con la salvedad de que la figura humana ocupa toda la imagen sin ser cortada en ningún punto.

Plano americano: Se denomina así al plano medio en que la figura humana aparece cortada de rodillas hacia abajo.

Plano medio: Muestra a la figura humana de cintura hacia arriba, o incluso de medio torso hacia arriba.

Primer plano: Muestra el rostro del personaje sin que éste sea cortado en ningún punto.

Gran primer plano: Muestra el rostro, pero en este caso, sí que aparece cortado, mostrando mucho más detalle que en el caso anterior.

Plano detalle: Muestra una parte del cuerpo muy ampliada.

3.- Tipos de angulación:

Se refiere al ángulo desde el cual se muestra la imagen. Cuando éste no es el punto de vista natural puede ser:

Angulo picado: Es el que se obtiene cuando la cámara se situa por encima del punto de vista habitual. Los personajes se ven desde arriba. Existe un picado extremo que se da cuando la cámara se situa encima de la cabeza del sujeto y enfocando de un modo paralelo al suelo y que se denomina ángulo cenital.

Ángulo contrapicado: Es aquel que se produce cuando la cámara se situa por debajo del punto de vista natural. Este ángulo se utiliza expresivamente para enfatizar la fuerza o el poder del sujeto. El ángulo contrapicado extremo, con el objetivo situado paralelo al suelo se denomina ángulo nadir.

Ángulo aberrante: Se toma inclinado la cámara, de modo que la línea de horizonte genera un ángulo marcado con respecto a la base de la fotografía.

Tema 13 Proporcionalidad

1. La proporción

Dos figuras guardan proporción si las partes de la primera se corresponden, en la misma relación de medida, con las partes de la segunda.

2. La igualdad

Se produce cuando dos figuras proporcionales tienen las mismas medidas. Un método para producir figuras iguales es la triangulación. Para ello, se debe descomponer la figura en triángulos y mediante el uso del compás, tomar medidas de cada uno de sus lados para copiarlos en la misma disposición que se encuentran en la figura original.

3. La semejanza

Se produce cuando dos figuras proporcionales tienen medidas distintas. En geometría, un modo de producir figuras semejantes es la radiación desde un punto. Para ello, se unen todos los vértices de la figura con un punto cualquiera A. Si, por ejemplo, queremos ampliar al doble de tamaño la figura, añadiremos la distancia que hay desde A hasta el punto B, prolongaremos la recta que pasa por estos dos puntos y añadiremos la distancia A-B a partir del punto B, para obtener el punto B' que genera el nuevo vértice de la figura semejante ampliada al doble de tamaño.

Además, para producir imágenes semejantes en dibujo de tipo más artístico, podemos recurrir a dibujar una cuadrícula sobre el dibujo original. Posteriormente, dibujaremos una cadrícula proporcional al tamaño al que se quiera ampliar o reducir el dibujo, y utilizando las líneas de ésta como referencia, realizaremos el dibujo definitivo.

Tema 12 Redes y módulos

1. Tramas.
Una trama es un conjunto regular de líneas que crean una estructura basada en formas básicas. Estas formas pueden ser triángulos, cuadrados, rectángulos, hexágonos, etc.

2. Módulos.

Un módulo es una figura más o menos sencilla que se repite una serie de veces sobre una trama. La combinación y repetición de módulos permite construir mosaicos.

Los módulos pueden combinarse entre sí para formar otro mayor, llamado "supermódulo".

3. Diseño de un módulo de "tesela" sobre una red cuadrada.

Para diseñar este tipo de módulo es necesario eliminar superficie en uno de los lados del cuadrado y añadir una superficie igual y en la misma posición en el lado opuesto.

Las teselas también se pueden realizar sobre otras redes como vemos a continuación.

Tema 11: Polígonos

Se llama polígono a una superficie cerrada y plana, formada por segmentos. Se clasifican según su número de lados en triángulos (3), cuadriláteros (4), pentágonos (5), hexágonos (6), heptágonos (7), octógonos (8), eneágonos (9), decágonos (10), undecágonos (11), dodecágonos (12), etc.
Si sus lados son iguales son polígonos regulares, mientras que si no lo son, se les llama polígonos irregulares.

Todos los polígonos tienen vértices, que son los puntos de unión entre dos rectas. Cuando son mayores de tres lados, todos los polígonos tienen dos o más diagonales, que son las rectas que unen dos vértices no consecutivos.

· DIVISION DE LA CIRCUNFERENCIA EN 3 Y 6 PARTES IGUALES.
Para dividir la circunferencia en 6 partes iguales, primero se dibuja la circunferencia; A continuación se dibuja un diámetro vertical y posteriormente, con la misma medida del radio y con centro en los extremos de diámetro se trazan dos arcos que cortan la circunferencia en los 6 puntos necesarios. Si se unen de 6 en 6 se obtiene un hexágono. Si se unen tres puntos no consecutivos, se obtiene un triángulo equilátero, y si con los tres puntos restantes dibujamos un 2º triángulo equilátero, se obtiene el hexágono estrellado.




· DIVISION DE LA CIRCUNFERENCIA EN 4 Y 8 PARTES IGUALES.
Si se dibujan dos diámetros perpendiculares se obtiene la división en 4 partes. Si además, dibujamos otros dos diámetros que formen un ángulo de 45º con respecto a los anteriores, se obtienen las 8 divisiones. Uniendo estos puntos, se puede obtener, el cuadrado, el octógono regular, o los dos tipos de octógonos estrellados.
- El octógono estrellado de paso 2, que se obtiene dibujando dos cuadrados solapados.
- El octógono de paso 3, que se obtiene uniendo vértices, dejando cada vez dos vértices libres (sin unir) hasta completar la estrella con las 8 líneas necesarias.

Tema 10: circunferencia

1. Círculo y circunferencia.

Se llama circunferencia a la curva cerrada y plana, cuyos puntos se mantienen a una distancia constante de otro, llamado centro.
Se llama círculo a la superficie contenida en la circunferencia.

2. Rectas notables de la circunferencia.

-Radio. Es la recta que va desde el centro de la circunferencia hasta un extremo. Es la mitad del diámetro. También se llama radio a la abertura de compás con la que dibujamos la circunferencia.

-Diámetro. Es la recta que cruza de parte a parte la circunferencia y que pasa por el centro. Es el doble del radio.

-Arco. Es una parte de la circunferencia.

-Cuerda. Es la línea recta que une los extremos de un arco.

-Flecha. Es la recta perpendicular a una cuerda y comprendida entre ésta y su arco.

-Tangente. Es la recta que toca solamente en un punto a la circunferencia.

-Secante. Es la recta que corta a la circunferencia en dos partes y que, por lo tanto, tiene dos puntos de contacto.


3. Posiciones relativas entre dos circunferencias.

Tema 9: Cuadriláteros

El cuadrilátero es una figura plana formada por cuatro rectas que se cortan entre sí. Se clasifican en dos grandes grupos:

PARALELOGRAMOS. Tienen los lados paralelos dos a dos.

-Con sus lados perpendiculares entre sí:

Cuadrado: Sus lados son iguales y sus diagonales son perpendiculares entre sí.
Rectángulo: Sus lados no son iguales y sus diagonales no son perpendiculares entre sí.

-Con sus lados no perpendiculares entre sí:

Rombo: Tiene los lados iguales y sus diagonales perpendiculares entre sí.
Romboide: Tiene los lados desiguales y sus diagonales no son perpendiculares entre sí.

NO PARALELOGRAMOS. Al menos dos lados no son paralelos entre sí.

-Trapecio: Todos los trapecios tienen dos lados paralelos.

Trapecio isósceles: Sus lados no paralelos son iguales.
Trapecio escaleno: Sus lados no paralelos son desiguales
Trapecio rectángulo: Tiene dos ángulos rectos.

-Trapezoide: No tiene ningún lado paralelo.

CASOS PRÁCTICOS:

Dibujar un cuadrado a partir de su lado.

Dibujar un rectángulo conociendo el lado menor y el lado mayor.

Dibujar un rombo conociendo su diagonal menor y su lado.

Dibujar un trapecio rectángulo conociendo dos lados perpendiculares y uno oblícuo.

Tema 8: Triángulos

El triángulo es una figura cerrada y plana formada por tres segmentos que se cortan entre sí. Por tanto, tiene tres lados, tres vértices, y la suma de sus tres ángulos es 180º. Los ángulos se designan con las letras griegas α, β y γ; los vértices se designan con letras mayúsculas, A, B, C, etc. y los lados opuestos se designan con letras minúsculas, a, b, c…

Tipos de triángulos según sus lados.

- Equilátero: los tres lados son iguales.

- Isósceles: solamente son iguales dos lados.

- Escaleno: no tiene ningún lado igual.

Tipos de triángulos según sus ángulos.

- Acutángulo: sus tres ángulos son agudos.

- Rectángulo: uno de sus ángulos es recto. Los lados del ángulo se llaman catetos y el lado opuesto al ángulo recto, hipotenusa.

- Obtusángulo: tiene un ángulo obtuso.

Rectas y puntos notables de un triángulo.

- Altura. Es la recta perpendicular a un lado, que pasa por el vértice opuesto. El punto en el que se cortan las alturas determina el ortocentro.

- Mediatriz. Es la recta que divide en dos partes iguales el lado de un triángulo. El punto donde se cortan las mediatrices de los lados determina el circuncentro que es el centro de la circunferencia en la que se inscribe el triángulo.

- Bisectriz. Es la recta que divide en dos partes iguales el ángulo de un triángulo. El punto donde se cortan las bisectrices de los ángulos determina el incentro que es el centro de la circunferencia inscrita y tangente a los lados del triángulo.

- Mediana de un triángulo. Es la recta que une el centro de un lado con el vértice opuesto. El punto en el que se cortan las tres medianas determina el baricentro, que es el centro de gravedad del triángulo.


Construcción de un triángulo equilátero conociendo el lado.

Construcción de un triángulo isósceles conociendo sus lados menor y mayor.

Construcción de un triángulo escaleno conociendo sus tres lados.

Construcción de un triángulo rectángulo conociendo un cateto y la hipotenusa.

Tema 7. Composición

1. Composición.

Es el proceso por medio del cual se ordenan los elementos visuales (puntos, líneas, planos, colores, etc.) en una imagen.

2. El formato.

Es la forma y el tamaño del soporte en el que se representa la imagen. Los formatos pueden ser muy variados y añaden expresividad a la imagen.

3. El esquema compositivo.

Es un conjunto de líneas sobre las que se sitúan y organizan los elementos de la imagen. Generalmente son invisibles y se pueden combinar entre ellas.

4. El movimiento en la composición.

Los elementos visuales representados en un dibujo pueden provocar un recorrido de la vista en una dirección determinada. El siguiente esquema ordena la cantidad de movimiento de las distintas direcciones básicas:

poco dinámico-----------------------------------------------------muy dinámico
horizontal----------------vertical----------------oblícuo-----------------curvado

5. El ritmo.

Como en la música, que organiza sonidos en el tiempo, las artes visuales organizan formas en el espacio creando sensaciones de repetición, alternancia, crecimiento o discontinuidad. Un ritmo consiste en la repetición de una forma sobre una misma representación artística. Los ritmos constituyen un recurso para generar dinamismo en una imagen, y si además se combinan con las diferentes direcciones básicas, se puede potenciar esa sensación.

6. El equilibrio y el peso visual.

Hablamos de peso visual cuando una forma atrae fuertemente nuestra atención. Un mismo elemento se considera más pesado cuanto más arriba y a la derecha se encuentra. Para componer una obra adecuadamente hay que tener en cuenta los diferentes pesos visuales con el fin de lograr el equilbrio.

Tema 6. Simetría

La simetría es una relación espacial entre dos figuras, en la que cada punto se corresponde con otro, de modo que ambos guardan la misma distancia con respecto a una línea, un punto o un plano.
En la naturaleza, aunque nada es exactamente simétrico, podemos encontrar varios casos, como las manos, la cara, mariposas, pájaros, etc. Veamos ahora varios tipos de simetría.

Simetría axial. Dos puntos simétricos llamados A y A’ están situados en la misma recta perpendicular a una línea llamada eje de simetría y a la misma distancia de ella y cada uno por un lado. Simetría central. Dos puntos simétricos llamados A y A’ están situados en la misma recta que pasa por un punto llamado centro de simetría y a la misma distancia de él y cada uno por un lado. Simetría radial. Es la combinación de las dos anteriores y se produce cuando varios ejes de simetría se cortan en un mismo punto que también es centro de simetría.

Tema 5. Trazados geométricos básicos

Los trazados geométricos básicos son operaciones que se realizan sobre el papel con diferentes materiales del dibujo técnico como la escuadra, el cartabón y el compás.

1. Mediatriz de un segmento:

La mediatriz es una recta perpendicular a un segmento y que corta a éste por el centro en dos partes iguales. Tiene la propiedad de que cualquiera de sus puntos se encuentran a la misma distancia de los dos extremos del segmento.

Para realizar la mediatriz hay que seguir los siguientes pasos:

1. Centramos el compás en cada uno de los extremos del segmento (puntos A y B) y realizamos dos arcos que se cortan en dos puntos (C y D)

2. Trazamos la mediatriz uniendo los puntos C y D.

2. Bisectriz de un ángulo

La bisectriz es la recta que divide a un ángulo en dos partes iguales. Tiene la propiedad de que cualquiera de sus puntos se mantienen a la misma distancia de los lados del ángulo en sentido perpendicular.

Para realizar la bisectriz hay que seguir los siguientes pasos:

1. Centramos el compás en el vértice y trazamos un arco que corta a los lados del ángulo en los puntos A y B.

2. Centramos el compás en los puntos A y B y trazamos dos arcos que se cortan entre sí en el punto C.

3. Dibujamos la bisectriz uniendo el vértice del ángulo con el punto C.

3. División de un segmento en partes iguales

Además del procedimiento matemático que consiste en medir el segmento y dividir el resultado en el número de partes que se quieran obtener, existe un método gráfico para el que no es necesario operar con números. Para ellos seguiremos los siguientes pasos.

1. A partir de un extremo del segmento (punto B), se traza una semirrecta de cualquier tamaño y con cualquier dirección.

2. Se toma una unidad con una medida cualquiera y a partir del extremo B del segmento y sobre la semirrecta que acabamos de dibujar, se sitúa esta medida tantas veces como divisiones queramos. La última división (punto C) se une con el extremo A del segmento.

3. Por todos los puntos situados sobre el segmento CB, se trazan rectas paralelas al segmento AC.

4. Suma de segmentos

1. Se dibuja una recta cualquiera y se situa un punto de origen A.
2. Con el compás, se toma la medida del segmento AB y se traslada sobre el punto A que hemos marcado en el paso anterior.
3. Se toma la medida del segmento BC y se traslada al punto B obtenido en el paso anterior.
4. La solución es el total que resulta de situar un segmento a continuación del otro.

5. Resta de segmentos

1. Se dibuja una recta cualquiera y se situa un punto de origen A.
2. Con el compás, se toma la medida del segmento AB y se traslada sobre el punto A que hemos marcado en el paso anterior.
3. Se toma la medida del segmento BC y se traslada al punto B obtenido en el paso anterior, pero debemos hacerlo marcano sobre la recta, a la izquierda del punto B.
4. La solución es la diferencia que resulta al comparar la dimensión de los dos segmentos ya que hemos situado el uno sobre el otro.

6. Suma de ángulos

1. Se dibuja una recta y se situa un punto O de origen.

2. Trazamos el mismo arco con una medida cualquiera sobre el ángulo alfa, el beta y sobre la recta.

3. Medimos con el compás la distancia entre los puntos 1 y 2 del ángulo alfa y la trasladamos sobre el arco que hemos trazado con centro en el punto O.

4. Medimos con el compás la distancia entre los puntos 2 y 3 del ángulo beta y la trasladamos sobre el arco anterior, con centro en el punto 2.

5. El resultado es el ángulo que tiene como lados las semirrectas que pasan por los puntos 1 y 3.

7. Resta de ángulos

1. Se dibuja una recta y se situa un punto O de origen.

2. Trazamos el mismo arco con una medida cualquiera sobre el ángulo alfa, el beta y sobre la recta.

3. Medimos con el compás la distancia entre los puntos 1 y 2 del ángulo alfa y la trasladamos sobre el arco que hemos trazado con centro en el punto O.

4. Medimos con el compás la distancia entre los puntos 2 y 3 del ángulo beta y la trasladamos sobre el arco anterior, con centro en el punto 2. Hay que prestar atención en un detalle. El arco hay que trazarlo con centro en el punto 3, pero hacia el punto 1.

5. El resultado es el ángulo que tiene como lados las semirrectas que pasan por los puntos 1 y 3

Tema 4. Paralelismo y perpendicularidad

1. Definiciones:

Rectas Paralelas: Son aquellas que llevan una misma dirección y que nunca se cortan.
Rectas perpendiculares: Son aquellas que se cortan formando ángulo de 90º.

2. Horizontal y Vertical:

Son las direcciones más habituales basadas en el paralelismo y la perpendicularidad. Estas direcciones forman módulos cuadrados y rectángulos que podemos encontrarnos en todas partes: papel, libros, billetes, paredes, edificios, etc.

3. La escuadra y el cartabón:

Son las plantillas que se utilizan para poder dibujar correctamente rectas paralelas y perpendiculares.